报告题目：QUANTITATIVE MATRIX-DRIVEN DIOPHANTINE APPROXIMATION ON M0-SETS

报告人：周青龙

负责人：冯妍

报告时间：2025年9月11日19；00到20：00

报告地点：腾讯会议，会议号：809 448 684

参加人员：教师，研究生

报告摘要：Let E ⊂ [0, 1)^d be a set supporting a probability measure μ with

Fourier decay |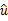(t)| ≪ (log |t|)^{−s} for some constant s > d + 1. Consider a

sequence of expanding integral matrices 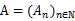such that the minimal

singular values of 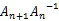are uniformly bounded below by K > 1. We

prove a quantitative Schmidt-type counting theorem under the following constraints:

(1) the points of interest are restricted to E; (2) the denominators of

the “shifted” rational approximations are drawn exclusively from A. Our result

extends the work of Pollington, Velani, Zafeiropoulos, and Zorin (2022) to

the matrix setting, advancing the study of Diophantine approximation on fractals.

Moreover, it strengthens the equidistribution property of the sequence

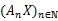for μ-almost every x ∈ E. Applications include the normality of

vectors and shrinking target problems on fractal sets.

报告人简介：周青龙，武汉理工大学理学院数学系副教授，硕士生导师，主要从事分形几何与动力系统、丢番图逼近与度量数论的研究工作。在期刊 IMRN、 ETDS、Nonlinearity等期刊发表论文多篇，主持国家自然科学基金青年基金。