变分分析与优化前沿论坛(7月5日下午)
学术报告（一）
报告题目：Exact continuous relaxations and algorithms for
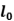regularized optimization problems
报告人：边伟 (哈尔滨工业大学)
报告时间：2022年7月5日14:30-
腾讯会议：394-2491-2514 密码：123123
参加人员：本科生、研究生、教师
报告摘要：In this talk, we considertwo classes of
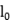regularized optimization problems, in which the group sparsity is considered.Firstly, we givethe continuous relaxation models of the considered problem and establish the equivalence of these two problems in the sense of global minimizers. Then, we define a class of stationary points of the relaxation problem, and prove that any defined stationary point is a local minimizer of the considered
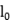regularized problem and satisfies a desirable property of its global minimizers. Further, based on the difference-of-convex (DC) structure of the relaxation problem, we designsome corresponding algorithms and provetheir convergence properties. Finally, some numerical experimentsare illustratedto show the efficiency of the proposed algorithms.
报告人简介：边伟，哈尔滨工业大学数学学院，教授、博士生导师。2004年和2009年于哈尔滨工业大学分别获得学士和博士学位，随后入职哈工大数学学院。2010-2012年访问香港理工大学跟随陈小君教授，从事博士后工作。主要从事的研究领域为：最优化理论与算法、神经网络。先后在 MP, SIOPT, SIIMS, SINUA，SISC,MOR和四个IEEE系列汇刊发表多篇学术论文。先后主持3项国家自然科学基金项目，并获得2018年度 “龙江青年学者”和2019年度国家级青年人才。现任中国运筹学会理事，中国运筹学会数学规划分会理事，黑龙江数学会常务理事，国际期刊JOTA编委。
学术报告（二）
报告题目：Newton method for the composite row sparsity regularized optimization
报告人：孔令臣 (北京交通大学)
报告时间：2022年7月5日15:10-
腾讯会议：394-2491-2514 密码：123123
参加人员：本科生、研究生、教师
报告摘要：This paper is concerned with the composite row sparsity regularized (cRSR) minimization problem, which captures a number of important applications arising in machine learning, statistics, signal and image processing, and so forth. Due to the non-convexity and discontinuity of the composite row sparsity regularization term, the cRSR problem is NP-hard in general. In this paper, we study the optimality conditions of the cRSR problem and derive its stationary equation which is crucial to design efficient algorithm. Based on this stationary equation, an easy-to-implement Newton method is designed to solve the cRSR problem (NcRSR for short). The quadratic convergence rate and iteration complexity estimation of the NcRSR are rigorously proved under some mild conditions. To demonstrate the effectiveness of NcRSR, we apply it to solve the simultaneous clustering and optimization and trend filtering problems. Extensive experimental results illustrate that our approach has superior performance comparing to the state-of-the-art methods. In particular, NcRSR possesses not only perfect clustering performance and estimation accuracy but also one hundred times faster than the first-order methods.
报告人简介：孔令臣博士，北京交通大学数学与统计学院，教授，博士生导师，中国运筹学会数学规划分会副秘书长。2007年毕业于北京交通大学，获博士学位。2007-2009年，加拿大滑铁卢大学组合与优化系博士后。2009年9月入职北京交通大学数学系，2010年晋升为副教授，2014年晋升为教授。主要从事统计优化、高维统计分析、稀疏优化、对称锥互补和优化问题以及医学和交通应用等方面的研究。主持国家自然科学基金面上项目和参与973课题、国家自然科学基金重点项目以及北京市自然科学基金重点项目等，获得2012度中国运筹学会青年奖。
学术报告（三）
报告题目：A New Augmented Lagrangian Method for MPCCs - Theoretical and Numerical Comparison with Existing Augmented Lagrangian Methods
报告人：郭磊 (华东理工大学)
报告时间：2022年7月5日16:00-
腾讯会议：394-2491-2514 密码：123123
参加人员：本科生、研究生、教师
报告摘要：We propose a new augmented Lagrangian (AL) method for solving the mathematical program with complementarity constraints (MPCC), where the complementarity constraints are left out of the AL function and treated directly. Two observations motivate us to propose this method: the AL subproblems are closer to the original problem in terms of the constraint structure; and the AL subproblems can be solved efficiently by a nonmonotone projected gradient method, in which we have closed-form solutions at each iteration. The former property helps us show that the proposed method converges globally to an M-stationary (better than C-stationary) point under MPCC relaxed constant positive linear dependence condition. Theoretical comparison with existing AL methods demonstrates that the proposed method is superior in terms of the quality of accumulation points and the strength of assumptions. Numerical comparison, based on problems in MacMPEC, validates the theoretical results.
报告人简介：郭磊，博士生导师，2013年博士毕业于大连理工大学，师从林贵华教授，2019年至今工作于华东理工大学。曾先后在上海交通大学、加拿大维多利亚大学、香港浸会大学等工作与合作研究。曾获得辽宁省优秀博士学位论文、教育部首届博士研究生国家奖学金等，主要从事最优化理论及应用研究，主持国家自然科学基金项目等多项，在Mathematical Programing、SIAM Journal on Optimization等重要期刊发表论文10余
学术报告（四）
报告题目：Towards Gradient-based Bilevel Optimization in Machine Learning
报告人：张进 (南方科技大学)
报告时间：2022年7月5日16:40-
腾讯会议：394-2491-2514 密码：123123
参加人员：本科生、研究生、教师
报告摘要：Recently, Bi-Level Optimization (BLO) techniques have received extensive attentions from machine learning communities. In this talk, we will discuss some recent advances in the applications of BLO. First, we study a gradient-based bi-level optimization method for learning tasks with convex lower level. In particular, by formulating bi-level models from the optimistic viewpoint and aggregating hierarchical objective information, we establish Bi-level Descent Aggregation (BDA), a flexible and modularized algorithmic framework for bi-level programming. Second, we focus on a variety of BLO models in complex and practical tasks are of non-convex follower structure in nature. In particular, we propose a new algorithmic framework, named Initialization Auxiliary and Pessimistic Trajectory Truncated Gradient Method (IAPTT-GM), to partially address the lower level non-convexity. By introducing an auxiliary as initialization to guide the optimization dynamics and designing a pessimistic trajectory truncation operation, we construct a reliable approximation to the original BLO in the absence of lower level convexity hypothesis. Extensive experiments justify our theoretical results and demonstrate the superiority of the proposed BDA and IAPTT-GM for different tasks, including hyper-parameter optimization and meta learning
报告人简介：张进南方科技大学数学系，助理教授，博士生导师，2007、2010年本科、硕士毕业于大连理工大学，2014年博士毕业于加拿大维多利亚大学。2015至2018年间任职香港浸会大学数学系，2019年初加入南方科技大学数学系。张进一直致力于最优化理论和应用研究，代表性成果发表在MP、SIOPT、SINUM、JMLR、IEEE TPAMI、ICML、NeurIPS等有重要影响力的应用数学、机器学习期刊与会议上。研究成果获得中国运筹学会青年科技奖，主持国家自然科学基金青年与面上项目、香港研究资助局面上项目、广东省自然科学基金杰青项目、深圳市科创委优青项目。
