2022年国家自然科学基金之天元数学优化讲习班
现代变分分析与数学优化
现代变分分析是数学领域的重要研究课题之一，已成为运筹学、计算数学、机器学习、压缩感知、最优控制与动力系统等领域研究的重要分析工具。随着大数据与人工智能时代的到来，客观实际问题呈现出规模大、结构复杂、不确定性、多属性与系统性。这些问题为现代变分分析与数学优化理论及其相关领域的深入研究带来了发展机遇，同时也给其带来了诸多挑战。为了推动变分分析与数学优化相关学科的发展，交流最新研究成果，促进学术合作与交流，带领年轻学者掌握现代变分分析和相关数学优化的基础研究方法和前沿研究手段，在国家自然科学基金数学天元基金与西南大学数学与统计学院等资助下，西南大学联合中国运筹学会主办拟定于2022年6月15日至2022年7月4日特推出“现代变分分析与数学优化讲习班”，并于2022年7月5日至2022年7月7日举办“变分分析与优化前沿论坛”。
本次讲习班邀请到国内外著名的中青年专家，为国内数学优化、计算数学、机器学习等方向的研究生开设变分分析与优化相关专题课程和优化前沿学术报告，同时介绍相关课题在国际上最新的研究理论和方法。
一、主办单位
西南大学、中国运筹学会
承办单位
西南大学数学与统计学院
二、讲习班委员会
学术委员会（按拼音排序）：
主席：戴彧虹研究员(中国科学院数学与系统科学研究院)
张伟年 教授(四川大学/西南大学数学与统计学院兼职学术院长)
成员：
林贵华教授（上海大学）
罗自炎 教授(北京交通大学)
宋文 教授（哈尔滨师范大学）
王宪福教授 (加拿大英属哥伦比亚大学)
张国川教授(浙江大学)
张立卫 教授(大连理工大学)
郑喜印 教授（云南大学）
周家足教授(西南大学)
组织委员会成员（按拼音排序）：
陈加伟 教授 (西南大学，召集人)
刘贤宁 教授 (西南大学，数学与统计学院常务副院长)
王建军 教授 (西南大学，数学与统计学院副院长)
易遵尧教授(西南大学，数学与统计学院党委书记)
张俊容副教授(西南大学)
会务组成员
刘亚丽，刘婕，宋丹，苏化升，杨蕊溪，郑金兰
三、报名条件
学员应具备一定的泛函分析、凸分析、非光滑分析与优化理论等基础的学者、硕士与博士研究生。
四、授课时间
2022年6月14日报到，6月15日至7月4日专题讲习班正式上课,7月5日-7月6日学术会议，7月7日自由讨论,7月8日离开。专题讲习班授课内容见附件1,课程安排见课程表。
五、授课方式与授课地点
本次讲习班采用线上为主,线上与线下方式相结合，线下授课地点为西南大学数学与统计学院学术报告厅(明德楼18楼会议室1802)。因疫情原因，线下学员不超过30人(仅限重庆市内)。备注：建议学员自带笔记本电脑。
六、食宿与费用
本讲习班不收取学员任何费用，免费提供相关学习资料，为所有线下学员提供工作餐，住宿自理。
七、联系人及方式
陈加伟(15123233235)、苏化生(13516355736) 邮箱：workshop2022swu@163.com
QQ群：280534633
微信群
附1：专题讲习班授课安排(暂定)
u 授课时间：2022年6月15日-6月20日(每天上午8：30-11：50，线上报告)
主讲教师：张立卫 教授(大连理工大学)
主讲内容：1.宇宙空间：方向点;地平锥;地平函数;强制性质。
2.集值映射: 集合列的外极限,内极限和收敛；
集值映射的外极限,内极限和收敛;上图收敛。
3.变分几何:
集合的切锥,正则切锥,正则法锥和法锥,外二阶切集合；
非线性优化约束集合的切锥和外二阶切集。
4.下半连续函数微分学:
函数的次导数,正则次导数,次梯度,正则次梯度,地平次微分；链式法则。
u 授课时间：2022年6月21日-6月24日(每天上午8：30-11：50，线上报告)
主讲教师：王宪福 教授（加拿大英属哥伦比亚大学）
主讲内容：Variational Analysis and Optimization：basic theory
1. Lower semicontinuous and Lipschitz functions:
Limsup and liminf,Lower semicontinuous functions,Weierstrass’ extremal value theorem,Lipschitz functions and convex functions,Support functions
2. Tangent and normal cones:
Clarke tangent cone and normal cone; Frechet normal cone;Limiting normal cone
3. Subdifferential and subdifferential calculus：
Frechet subdifferential and limiting subdifferential；Subderivatives and Clarke’s subdifferential； Calculus
4. Moreau envelope and proximal mappings：
Moreau envelopes；Moreau envelope of convex functions and nonconvex functions；Proximal mappings
5. Optimality conditions and regularities
The Lagrange multiplier rule； Direction of complete descent；Metric regularity and sub-regularity of subdifferential mappings
6. Subgradient methods
Local convergence of alternative projections；Sparsity optimization；
Forward-reflected-backward splitting method for nonconvex minimization problems
u 授课时间：2022年6月25日-6月26日(腾讯会议线上报告)
主讲教师：宋文 教授（哈尔滨师范大学）
主讲内容：1. 经典最优化条件回顾，上图导数、切锥、法锥及其基本性质。
2. 抛物正则与二阶上图可微性
3. 次导链式法则
4. 复合优化问题的二阶最优性条件
u 授课时间：2022年6月27日-6月29日(腾讯会议线上报告)
主讲教师：罗自炎 教授等北京交通大学优化团队（北京交通大学）
主讲内容：变分分析与稀疏优化，主要内容包括：
1.Introduction to sparse optimization
2.Optimization theories on
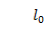-norm related sparse optimization
3.A Lagrange–Newton algorithm for sparse nonlinear programming
4.A gradient projection subspace pursuit (GPSP) algorithm for doublesparsity
constrained optimization
5.A semismooth Newton-based augmented Lagrangian method for a sparse and grouping promoted least squares problem
u 授课时间：2022年6月30日-7月1日(腾讯会议线上报告)
主讲教师：林贵华 教授（上海大学）
主讲内容：1.非合作博弈及其求解方法；
2. 主从博弈及其求解方法。
u 授课时间：2022年7月2日-7月4日(腾讯会议线上报告)
主讲教师：郑喜印 教授（云南大学）
主讲内容：变分分析中的度量正则性与度量次正则性，包括：
1.切锥、法锥和次微分及其主要性质回顾，
2度量正则性；
3.度量次正则性；
4.扰动分析。
讲习班教材及参考文献：
[1]H. H. Bauschke, D.R. Luke, H. M. Phan, X. Wang, Restricted normal cones and
sparsity optimization with affine constraints, Found. Comput. Math. 2014,14:63-83
[2]F.H. Clarke, Optimization and Nonsmooth Analysis, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1990.
[3]J. Frédéric Bonnans，Alexander Shapiro，Perturbation Analysis of Optimization Problems，Springer，2000
[4]H. Gfrerer, B.S. Mordukhovich, Second-order variational analysis of parametric
constraint and variational systems, SIAM J. Optim., 2019, 29:423-453
[5]B. S. Mordukhovich, Variational Analysis and Generalized Differentiation, I: Basic
Theory, II: Applications, Springer, Berlin, 2006.
[6]B.S. Mordukhovich, T. Nghia, Second-order variational analysis and characterizations of tilt-stable optimal solutions in infinite-dimensional spaces， Nonlinear Anal. 2013, 86:159-180
[7]B.S. Mordukhovich, J.V. Outrata，C.H. Ramírez, Second-order variational analysis
in conic programming with applications to optimality and stability, SIAM J. Optim.,
2015, 25(1):76--101
[8]B.S. Mordukhovich, Variational Analysis and Applications, Springer, Cham, Switzerland, 2018
[9]R.T. Rockafellar, R. J-B. Wets, Variational Analysis, Springer, Berlin, 1998.
[10]R.T. Rockafellar, Second-order variational analysis and its role in optimization.
https://sites.math.washington.edu/~rtr/papers/rtr233-SecondOrderVA.pdf
[11] 张立卫,吴佳,张艺, 变分分析与优化,科学出版社, 北京,2019
[12] Ziyan Luo, Defeng Sun*, Kim-Chuan Toh and Naihua Xiu, Solving the OSCAR and
SLOPE models using a semismooth Newton-based augmented Lagrangian method,
[13] Journal of Machine Learning Research, 20 (106) (2019) 1-25
[14] Lili Pan*, Ziyan Luo and Naihua Xiu, Restricted Robinson constraint qualification and optimality for cardinality-constrained cone programming, Journal of Optimization Theory and Applications, 175(1) (2017) 104-118
[15]赵晨,罗自炎,修乃华, 稀疏优化理论与算法若干新进展,运筹学学报,2020,24:1-24
[16]Chen Zhao, Ziyan Luo, Weiyue Li, Hou-duo Qi and Naihua Xiu, Lagrangain duality
and saddle points for sparse linear programming, Science China Mathematics, 62(10)
(2019) 2015-2032
[17]Chen Zhao, Naihua Xiu, Hou-duo Qi and Ziyan Luo*, A Lagrange–Newton algorithm
for sparse nonlinear programming, Mathematical Programming, Online, 2021.
https://doi.org/10.1007/s10107-021-01719-x
[18]Shenglong Zhou*, Ziyan Luo, Naihua Xiu and Geoffrey Ye Li, Computing one-bit
compressive sensing via double-sparsity constrained optimization, IEEE Transactions
on Signal Processing, 70(2022) 1593-1608
[19]X.Y. Zheng, Attainable separation property and asymptotic hyperplane for a closed
convex set in a normed space, J. Math. Anal. Appl. 2020,489:124121
