非线性泛函分析学术报告

报告一

报告题目：Sharp criteria for nonlocal elliptic inequalities on manifolds

报 告 人：孙玉华 教授（南开大学）

报告时间：2024年12月20日（星期五）14:30-15:10

报告地点：数学大楼912

参加人员：教师、研究生、本科生

报告摘要：We investigate the existence and nonexistence to nonlocal differential inequalities on manifolds. This talk is based on joint work with Qingsong Gu, and Xueping Huang.
报告人简介：孙玉华，南开大学数学学院教授，博士生导师，研究方向为黎曼流形及图上的分析，包括椭圆及抛物方程，在包括CPAM，JFA, Math. Annalen, JAM， CVPDE等著名期刊发表学术论文20余篇。曾获得天津市数学会与统计学联合学术年会“青年学者奖”，入选天津市131创新型人才培养工程第三层次名单。

报告二

报告题目：Energy quantization of the two dimensional Lane-Emden equation with vanishing potentials

报 告 人：陈志杰 教授（清华大学）

报告时间：2024年12月20日（星期五）15:10-15:50

报告地点：数学大楼912

参加人员：教师、研究生、本科生

报告摘要：In this talk, I will introduce some results about the concentration phenomena of the Lane-Emden equation with vanishing potentials. The type example is the well-known Henon equation. Comparing to the Lane-Emden case, the problem becomes much more complicated since a singular Liouville equation appears as a limit problem. As applications, we give the complete asymptotic behavior of ground state solutions for the Henon equation.
报告人简介：陈志杰，2013年清华大学博士毕业，2013-2016年台湾大学博士后，目前任清华大学数学系、丘成桐数学中心教授，博士生导师，清华大学求真书院副院长，2017年获得清华大学学术新人奖(清华大学四十周岁以下教师最高奖励)，2018年获得ICCM最佳论文奖，入选国家级青年人才，研究方向为非线性偏微分方程和复变量常微分方程，在耦合薛定谔方程组、平均场方程、陈-西蒙斯方程组、古典爱森斯坦级数等方面做出了重要的成果，首次建立平均场方程与可积系统中Painleve方程的深刻联系，迄今已发表论文40多篇，部分论文发表在Adv.Math、Amer.J.Math、Arch.Ration.Mech.Anal、Comm.Math.Phys、J.Differ.Geom、Math.Ann等著名期刊。

报告三

报告题目：Infinitely many sign-changing normalized solutions for nonlinear scalar field equations

报 告 人：钟学秀 研究员（华南师范大学）

报告时间：2024年12月20日（星期五）16:00-16:40

报告地点：数学大楼912

参加人员：教师、研究生、本科生

报告摘要：We study the existence of infinitely many sign-changing solutions to the following nonlinear scalar Schrodinger equation

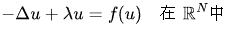
with a prescribed mass 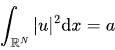Here 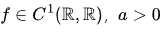is a given constant and 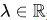is an unknown parameter appearing as a Lagrange multiplier. Jeanjean and Lu have established the existence of infinitely many sign-changing normalized solutions in [Nonlinearity 32 (2019), no. 12, 4942--4966] and [Calc. Var. Partial Differential Equations 59 (2020), no. 5, Paper No. 174, 43 pp.] for N=4 or 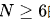. After fully utilizing the properties of positive solutions given by Jeanjean,Zhang and Zhong[J. Math. Pures Appl. (9) 183 (2024), 44--75], we give an alternative approach and extend the existence of infinitely many sign-changing normalized solutions to all .

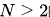报告人简介：钟学秀研究员，博士生导师。2015博士毕业于清华大学；2015-2017台湾大学博士后；2017-2019中山大学专职科研人员；2019为华南师范大学副研究员，华南数学应用与交叉研究中心青年拔尖引进人才；2024年7月破格晋升研究员并于同年获得博士生导师资格。研究方向是非线性泛函分析及其应用，目前的研究兴趣在于非线性椭圆型偏微分方程（以及方程组）的规范化解问题，包括解的存在性（不存在性）、唯一性（多解性）以及解的渐近行为分析（极限性态的刻画）等。目前已在J. Differential Geom., J. Math. Pures Appl., Math. Ann., Ann. Sc. Norm. Super. Pisa CI. Sci. (5), Calc. Var. Partial Differential Equations, J. Differential Equations, Sci. China Math. 等国内外重要期刊上发表多篇学术论文，其中有3篇ESI高被引论文。出版专著《偏微分方程中的分析学基础》一本。主持国家面上项目和青年项目各一项。在非线性泛函分析和椭圆偏微分方程领域的Li-Lin公开问题，Sirakov公开问题。Bartsch- Jeanjean-Soave公开问题等方面获得重要进展。

报告四

报告题目：哈密顿系统与辛动力系统中的闭轨道问题

报 告 人：刘会 教授（武汉大学）

报告时间：2024年12月20日（星期五）16:40-17:20

报告地点：数学大楼912

参加人员：教师、研究生、本科生

报告摘要：闭轨道的存在性、多重性和稳定性的研究是哈密顿系统与辛动力系统的核心内容之一，本报告主要介绍哈密顿能量面上闭特征、切触流形上Reeb闭轨道、Finsler流形上闭测地线等闭轨道问题的研究背景及我们的研究成果。

报告人简介：刘会，武汉大学数学与统计学院教授。2007年本科毕业于南开大学数学试点班，2012年博士毕业于南开大学陈省身数学研究所，2012年7月至2016年6月在中国科学技术大学工作，2016年7月至今任职于武汉大学。研究领域为哈密顿系统、非线性分析与辛几何，涉及理论包括Maslov型指标理论、Morse与Floer理论、嵌入切触同调理论等，并已在Geom. Topol., Trans. AMS, Adv. Math, J. Funct. Anal., Calc. Var. PDEs, Math. Z., J. Diff. Equ.等数学期刊上发表论文30余篇, 得到国家基金委优秀青年基金、面上项目等资助。